Бородкин Л.И. .
Математические методы и компьютер в задачах атрибуции текстов
(От Нестора до Фонвизина. Новые методы определения авторства.
под редакцией Л.В. Милова. М., "Прогресс", 1994, глава 2)
В предыдущей главе методика атрибуции текстов на основе анализа частот парной встречаемости грамматических классов слов была изложена на содержательном уровне. Опыт практического использования этой методики в задачах атрибуции древнерусских текстов подвел к строгой операционализации всех этапов ее реализации. В данной главе мы приводим формализованное, математическое описание методики, что позволяет не только придать точный смысл вводимым понятиям и процедурам, но и создает возможности для разработки компьютерных программ, реализующих предложенную методику атрибуции.
Как уже отмечалось в главе 1, частоты парной встречаемости грамматических слов рассматриваются различными авторами как существенные характеристики формальной структуры авторского текста. Так, В. Фукс в своей работе, посвященной анализу стилевых характеристик библейских текстов, отмечает: "Частоты переходов для синтаксических классов слов играют в исследованиях подлинности текстов чрезвычайно важную роль" [1].
Определив матрицу частот переходов для каждого изучаемого библейского текста, В. Фукс вводит в рассмотрение индекс различия Р, который вычисляется для пары текстов как сумма мер различия по всем соответствующих клеткам двух матриц. Значения индекса показывают в частности, что фрагменты "Евангелия от Иоанна" обладают большим сходством и сильно отличаются от "Апокалипсиса"; "Деяния апостолов" обнаруживают внутреннее единство, а "Евангелие от Луки" - несколько меньшее единство. Различия между "Евангелием от Луки" и "Деяниями апостолов" значительны, но выражены не столь отчетливо, как в случае "Евангелия от Иоанна" и "Апокалипсиса".
С помощью индекса Р Фуксу удалось четко различить стилевые особенности всех четырех канонических евангелических текстов. Однако попытки использовать этот и подобные ему коэффициенты для оценки близости стилевых характеристик древнерусских текстов оказались безуспешными в силу указанной выше специфики этих текстов. "Коэффициент Фукса" мог зачастую давать меньшую оценку степени близости двух фрагментов из одного произведения, чем двух текстов разных авто-ров. Дело в том, что суммирование незначительных различий при сравнении элементов двух матриц большого размера приводит к тому, что небольшое число действительно важных различий "тонет" в массе второстепенных деталей. Чтобы избежать этого, мы положили в основу методики атрибуции построение графа "сильных связей", конструируемого по матрице частот парной встречаемости грамматических классов слов.
Для получения такой матрицы необходимо:
- выбрать систему грамматических классов, достаточно детально описывающую грамматические особенности языка изучаемого периода;
- перекодировать последовательность слов анализируемого текста в последовательность соответствующих обозначений грамматических классов;
- вычислить частоты парной встречаемости для каждой пары классов с учетом направления развертывания текста (слева направо), т. е. построить искомую матрицу А частот парной встречаемости на уровне грамматических классов в данном тексте.
Мы исходим из гипотезы о том, что стиль автора проявляется в его "пристрастии" к определенным грамматическим связям, частота появления которых в тексте высока (им соответствуют высокие значения элементов aij матрицы А). Основная же масса элементов матрицы А соответствует слабым, несущественным статистическим связям на уровне грамматических классов; частоты этих связей малы (aij = 1..2), а их появление в сильной мере случайно (ведь объем исследуемых текстов ограничен). Поэтому привлечение этих "несущественных" связей на уровне грамматических классов в процессе атрибуции может только исказить результаты. Атрибуция же должна основываться на учете "существенных" связей, которым соответствуют высокие значения частот aij.
Итак, пусть рассматривается несколько гипотез об авторстве исследуемого текста, и для каждого предполагаемого автора имеются безусловно принадлежащие ему тексты. Тогда методика предлагаемой атрибуции описывается следующей схемой:
- Для каждого из имеющихся текстов (в том числе и для исследуемого текста) получаем матрицу А частот парной встречаемости на уровне грамматических классов (статистических связей).
- Анализируя каждую матрицу, выделяем для каждого текста совокупность грамматических связей с высокими (т.е. превышающими некоторое пороговое значение) частотами.
- При сравнении полученной совокупности "существенных" связей исследуемого текста с остальными определяется автор, чей текст характеризуется наиболее близкой по некоторому критерию совокупностью "существенных" грамматических связей.
В том случае, когда предполагается вводить в анализ "общую часть", или "ядро", в методику встраиваются два дополнительных пункта [2].
Конкретизацию описанной схемы атрибуции удобно провести, формализовав введенные понятия совокупности существенных грамматических связей, "общеязыкового ядра", критерия сравнения и т. д. Адекватный язык для такой формализации дает теория графов.
Основным понятием для даль-нейшего изложения будет понятие графа сильных связей, с помощью которого задается совокупность синтаксических связей с высокими частотами. Будем обозначать такой граф G(X,V), где Х - множество вершин, а V - множество дуг графа сильных связей.
Граф сильных связей Ga (X, V) строится по матрице А следующим образом. Каждому i-му синтаксическому классу ставится в соответствие вершина Xi графа Ga (X,V). Для формирования множества V дуг графа Ga (X, V) назначается некоторый порог 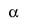 , и тогда все связи aij (i, j = 1,..., n) оказываются "разрезанными" на сильные (
, и тогда все связи aij (i, j = 1,..., n) оказываются "разрезанными" на сильные (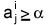 ) и слабые (
) и слабые (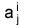 <
< 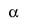 ). Каждой сильной связи
). Каждой сильной связи 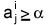 ставится в соответствие дуга графа Ga (X,V), идущая из вершины xi в вершину xj. Очевидно, чем больше величина порога
ставится в соответствие дуга графа Ga (X,V), идущая из вершины xi в вершину xj. Очевидно, чем больше величина порога 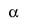 , тем меньше дуг содержит граф Ga (X,V) [З].
, тем меньше дуг содержит граф Ga (X,V) [З].
Пусть построены матрица A0 частот парной встречаемости грамматических классов для исследуемого текста и m матриц Ai (i = 1, ... m) для текстов, принадлежащих m известным авторам. Задавшись некоторым порогом 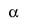 , построим графы сильной связи Gi(X,Vai) для каждой из матриц Ai(i= 0, 1, ..., m). Анализируя эти графы, выделим "общеязыковое ядро", т. е. граф Гa, составленный из таких дуг vi
, построим графы сильной связи Gi(X,Vai) для каждой из матриц Ai(i= 0, 1, ..., m). Анализируя эти графы, выделим "общеязыковое ядро", т. е. граф Гa, составленный из таких дуг vi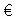 vai, которые входят в множество дуг Vaiне менее, чем l графов Gi(X,Vai),i
vai, которые входят в множество дуг Vaiне менее, чем l графов Gi(X,Vai),i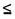 m. Далее произведем операцию "удаления" полученного графа Гa из каждого графа Gi(X,Vai), в результате чего получим графы
m. Далее произведем операцию "удаления" полученного графа Гa из каждого графа Gi(X,Vai), в результате чего получим графы 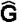 i(X,Vai), содержащие "существенные" синтаксические связи:
i(X,Vai), содержащие "существенные" синтаксические связи: 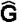 i(X,Vai)=
i(X,Vai)=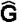 i(X,Vai)/Гa i = О, 1, ..., m
i(X,Vai)/Гa i = О, 1, ..., m
Для проверки гипотез о принадлежности исследуемого текста к одному из рассматриваемых авторов следует в соответствии с описанной выше схемой сравнить граф 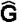 0(X,Vai) с графами
0(X,Vai) с графами 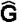 i(X,Vai). Учитывая специфику изучаемых текстов (в частности, вмешательство в авторский текст переписчиков, редакторов и т. д.), критерий для такого сравнения должен опираться не на детальное сопоставление дуг и вершин графов
i(X,Vai). Учитывая специфику изучаемых текстов (в частности, вмешательство в авторский текст переписчиков, редакторов и т. д.), критерий для такого сравнения должен опираться не на детальное сопоставление дуг и вершин графов 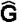 0(X,Vai) и
0(X,Vai) и 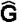 i(X,Vai) (i=1, ..., m), а на более общие, "интегральные" характеристики структуры этих графов.
i(X,Vai) (i=1, ..., m), а на более общие, "интегральные" характеристики структуры этих графов.
В данной работе критерий близости графов 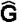 0(X,Vai) и
0(X,Vai) и 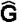 i(X,Vai) (i = 1, ..., m) предлагается строить, используя понятие "узловых вершин" этих графов (будем называть их далее узлами).
i(X,Vai) (i = 1, ..., m) предлагается строить, используя понятие "узловых вершин" этих графов (будем называть их далее узлами).
Узел yi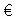 Х определим как такую вершину графа
Х определим как такую вершину графа 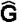 i(X,Vai) ) (i = 1, ...,m), в которую входит более чем
i(X,Vai) ) (i = 1, ...,m), в которую входит более чем 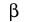 дуг. Таким образом, узлу данного графа
дуг. Таким образом, узлу данного графа 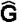 i(X,Vai) соответствует такой грамматический класс слов, который имеет существенные связи более чем с
i(X,Vai) соответствует такой грамматический класс слов, который имеет существенные связи более чем с 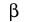 классами данного текста. Множество узлов графа
классами данного текста. Множество узлов графа 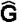 i(X,Vai) будем обозначать Yi.
i(X,Vai) будем обозначать Yi.
Введем критерий близости исследуемого текста к i-му тексту (i = 1, ..., m) как отношение числа общих для данных двух текстов узлов к суммарному количеству узлов для этих двух текстов: 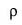 0i=|Y0
0i=|Y0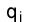 Yi|/|Y0
Yi|/|Y0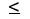 Yi| , i = 1, ..., m. (1)
Yi| , i = 1, ..., m. (1)
Как видно из формулы (1), значение коэффициента 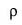 заключено в границах от 0 до 1. В том случае, если сравниваемые тексты не имеют общих узлов,
заключено в границах от 0 до 1. В том случае, если сравниваемые тексты не имеют общих узлов, 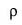 =О; если множества их узлов совпадают,
=О; если множества их узлов совпадают, 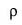 =1.
=1.
Чем больше доля их общих узлов, тем ближе значение 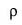 к 1. Если для некоторого i*-гo текста значение
к 1. Если для некоторого i*-гo текста значение 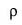 oi>
oi>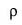 0j (j = 1, ..., m; j
0j (j = 1, ..., m; j 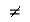 i*), то принимается гипотеза о принадлежности исследуемого текста i*-му автору.
i*), то принимается гипотеза о принадлежности исследуемого текста i*-му автору.
Для описания методики выявления авторских особенностей стиля нам потребуется ввести понятие общего графа G (X, U) для данной совокупности графов Gi(X,Vi) (i = 1,..., k). Множество дуг U общего графа G (X, U) определим как пересечение множеств Vi(i = 1,...,k): U = 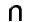 Vi. Таким образом, общий граф G (X,U) построен на таких дугах, которые содержатся во всех графах Gi(X,Vi) (i = 1, ..., k) [4].
Vi. Таким образом, общий граф G (X,U) построен на таких дугах, которые содержатся во всех графах Gi(X,Vi) (i = 1, ..., k) [4].
Введем также коэффициент qi, близости каждого из графов G (X,Vi) (i = 1, ..., k) к общему графу G (X, U) как отношение числа дуг, общих для графов Gi(X,Vi) и G (X, U), к числу дуг графа Gi(X,Vi): qi=|Vi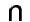 U| / |Vi|, i = 1. ..., k. (2)
U| / |Vi|, i = 1. ..., k. (2)
Коэффициент q изменяется в преде-лах 0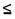 qi
qi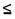 1; qi=1 , если все дуги общего графа имеются на графе Gi(X,Vi).
1; qi=1 , если все дуги общего графа имеются на графе Gi(X,Vi).
Еще одна модификация методики атрибуции связана с идеей построения "динамической выборки" текста атрибутируемого произведения. В этом случае выделяется достаточно большой фрагмент текста, и первая выборка совпадает с началом этого фрагмента. Далее граница выборки фиксированной длины "скользит" внутри фрагменты по ходу развертывания текста, каждый раз "перекрывая" частично предыдущую выборку. Тем самым удается проследить динамику и степень изменений большого фрагмента анализируемого текста и оценить его однородность.
Для пояснения смысла коэффициентов 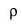 и q близости пары графов рассмотрим иллюстративный пример. Пусть имеются три графа связей с Множеством вершин (грамматических классов) Х={1, 2, 3, 4, 5, 6}:
и q близости пары графов рассмотрим иллюстративный пример. Пусть имеются три графа связей с Множеством вершин (грамматических классов) Х={1, 2, 3, 4, 5, 6}:
|
Определим узел графа как такую вершину, в которую входит не менее трех дуг. Тогда множество узлов графа G1 составляют вершины 2 и 5, графа G2 - вершины 2 и 4, а графа G3 - 2, 5 и 3
Перепишем формулу (1) в более простом виде: 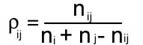 где ni, nj - число узлов i-го и j-го графов соответственно; nij - число общих узлов в сравниваемых графах. Легко видеть, что вычисления по формуле (3) дают для рассматриваемых графов G1,G2, G3 следующие значения: где ni, nj - число узлов i-го и j-го графов соответственно; nij - число общих узлов в сравниваемых графах. Легко видеть, что вычисления по формуле (3) дают для рассматриваемых графов G1,G2, G3 следующие значения:
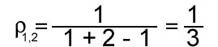 ; ;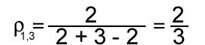 ; ;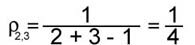
Таким образом, наиболее близкой (по критерию 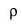
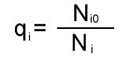 , (4) , (4)
где Ni0 - число общих дуг на графах Gi, G0. G0 - общий граф; Ni - число дуг на графе Gi .
Определим G0 - общий граф для G1, G2 G3.
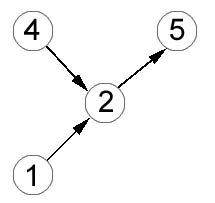
Вычисления по формуле (4) приводят к следующим результатам сравнения структурной близости каждого из графов G1, G2, G3 с общим графом G0 :
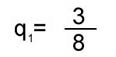 ; ;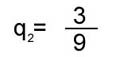 ; ;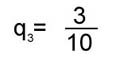
Самым близким (по критерию q) к общему графу оказывается граф связей первого текста, самым далеким - третьего.
Обобщив формулу (4), можно ввести в рассмотрение коэффициент ~qij , измеряющий близость структуры любой пары графов Gi и Gj, как отношение числа дуг, общих для графов Gi и Gj, к суммарному числу различающихся дуг для рассматриваемой пары текстов:
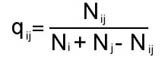 , (5) , (5)
Вычисления по формуле (5) дают следующие значения для сравнения структурной близости G1, G2и G3:
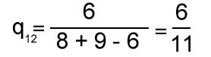 ; ;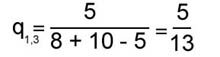 ; ;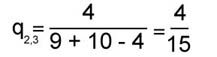
Ближе всего по совокупности связей оказываются первый и второй тексты, дальше всего - второй и третий.
Описанные методики были реа-лизованы в виде программ для ЭВМ. В 1973 г. была разработана программа для большой ЭВМ (БЭСМ-6) (на языке ФОРТРАН), и вплоть до 1988 г. обработка текстового материала производилась с помощью этой программы на ВЦ АН СССР и в НИВЦ МГУ. В 1989 г. была создана новая версия этой программы для персональных компьютеров, совместимых с IBM PC/AT, и с этого времени обработка текстов велась в лаборатории исторической информатики кафедры источниковедения Исторического факультета МГУ.
Предложенная нами методика атрибуции была использована позднее другими авторами в задачах определения авторства различных текстов.
Так, данный метод применялся Е. В. Злобиным при анализе "Записок" декабриста И. И. Горбачевского, члена общества "Соединенных славян" [5]. Авторство "Записок" долгое время вызывало споры. Итоги компьютерной обработки текстового материала не подтвердили принадлежности "Записок" перу И. И. Горбачевского.
Частоты взаимной встречаемости грамматических форм и графы сильных связей использовались А.В.Быстровым и Е.В.Злобиным в задаче атрибуции предсмертного письма Б.В.Савинкова [6]. Сравнительному анализу подверглись тексты Б.В.Савинкова и Я.Г.Блюмкина и собственно предсмертное письмо. Сочетание выводов, полученных с помощью компьютерного анализа, и результатов традиционного атрибутирования позволило отклонить гипотезу об авторстве Блюмкина.
Другой пример использования описанной выше методики атрибуции характеризует ее возможности при исследовании галльских панегириков [7]. Речь идет о работе И.Ю.Шабаги, изучавшей тексты сборника "XII Panegyrici Latini", являющегося од-ним из крупнейших источников по истории Поздней Римской империи. Первая из входящих в него речей - "Панегирик" Плиния Младшего императору Траяну (100 г.). Остальные 11 речей принадлежат галльским ораторам III - IV вв. и посвящены различным императорам. Авторы пяти панегириков известны (их имена сохранились в заголовках или в текстах речей); остальные шесть речей сборника не атрибутированы. Выделив для анализа галльских панегириков 40 грамматических классов, И. Ю. Шабага выявила "общеязыковое ядро" панегириков; его составляли как связи, присущие структуре латинского языка, так и связи, отражающие стилистические особенности панегирического жанра. Удаление общеязыкового ядра сохранило большую структурную близость галльских панегириков; коэффициент близости, измеряющий отношения совпадающих дуг в графах сильных связей каждой пары речей к общему их числу в том и другом панегирике, колебался от 0.14 до 0.35 на всем массиве анализируемых текстов.
|
|
Полученные результаты позволили автору работы сделать вывод о принадлежности второго и третьего панегириков одному автору - Мамертину и показали несостоятельность теории О. Зеена, уже более 100 лет приписывающей IV, VI, VII, VIII и IX панегирики перу Евмения - автора V панегирика. Как следует из результа-тов применения методики атрибуции, каждая из пяти указанных анонимных речей сборника принадлежит отдельному автору.
Таким образом, накапливающийся опыт использования предложенной методики атрибуции текстов дает основания говорить о широком диапа-зоне ее возможностей, имея в виду временной, пространственный и жанровый аспекты проблемы атрибуции.
ПРИМЕЧАНИЯ
1. Фукс В. По всем правилам искусства (точные методы в исследованиях литературы, музыки и изобразительного искусства // Искусство и ЭВМ. М., "Мир", 1975. Гл.VI. К тексту
2. Эти дополнительные пункты таковы: 2а) Сравнивая полученные совокупности грамматических связей, выделя-ем так называемое общеязыковое ядро, т.е. набор таких связей, которые содержатся во всех (или почти во всех) текстах. 26) Сформированное "общеязыковое ядро" удаляется из каждой совокупности отобранных грамматических связей с высокими частотами; оставшиеся после этого "существенные" статистические связи каждой совокупности уже в большей мере характеризуют авторский стиль. К тексту
Так называемое общеязыковое ядро в исследованиях разного масштаба играет разную роль. При исследовании произведений одного автора - это наиболее характерные особенности его стиля. При исследовании произведений определенного жанра, но разных авторов - это черты, свойственные прежде всего жанру, и т.д.
3. См. пример в главе I.К тексту
4. Очевидно, понятие общего графа совпадает с введенным ранее понятием "общеязыкового ядра" при l = m. К тексту
5. 3лобин Е.В. К вопросу об авторстве "Записок" И.И.Горбачевского // История СССР. № 2. С.140-155.К тексту
6. Быстров А.В., 3лобин Е.В. К вопросу об авторстве предсмертного письма Б.В.Савинкова - опыт комплексного исследования // Круг идей: Новое в исторической информатике. М., 1994. С.129-133. К тексту
7. Шабага И. Ю. Опыт исследования галльских панегириков количественными методами // Вестник Древней истории. 1993. № 1. С.147-161. К тексту
|